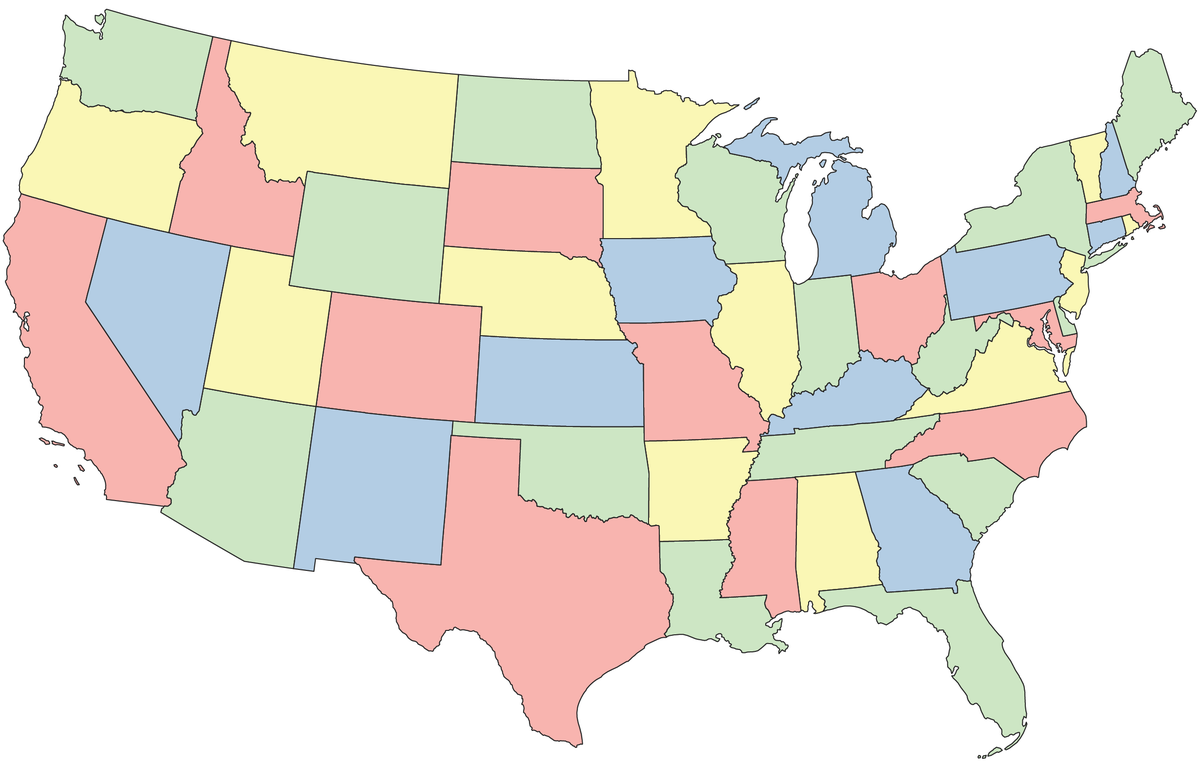
Four colour problem
It’s hard to prove mathematically, but it’s not very hard to wrap your brain around. In 2 dimensional space, it is impossible to draw five shapes that all touch each other with a contiguous border. Try it. Once you have four or more shapes, making the four touch requires that one shape be fully enveloped. You could have one shape touch as many shapes as you like, but those shapes cannot be touching more than three of the other shapes.
Are their exotic 2D geometries that work? Like, for example, the surface of a Klein bottle? (A cursory google search rules out the Klein bottle – any others perhaps?)
On a torus, you can have up to seven mutually adjacent regions. See https://upload.wikimedia.org/wikipedia/commons/3/37/Projection_color_torus.png